Oldschool

Jüngst begab es sich, dass Sohnemann mit einer Schulaufgabe nicht weiter wusste (man muss ja schon dankbar sein, wenn sie überhaupt fragen). Wie viele fünfstellige Zahlen lassen sich aus einer Menge von sieben Ziffern bilden? Bedingung: Keine der Ziffern darf sich innerhalb der Zahlen wiederholen. Schreibe alle möglichen Varianten auf. Papi hirntot vom Arbeitstag (und auch vom Feierabendbier) aber: geil, eine Denkaufgabe!

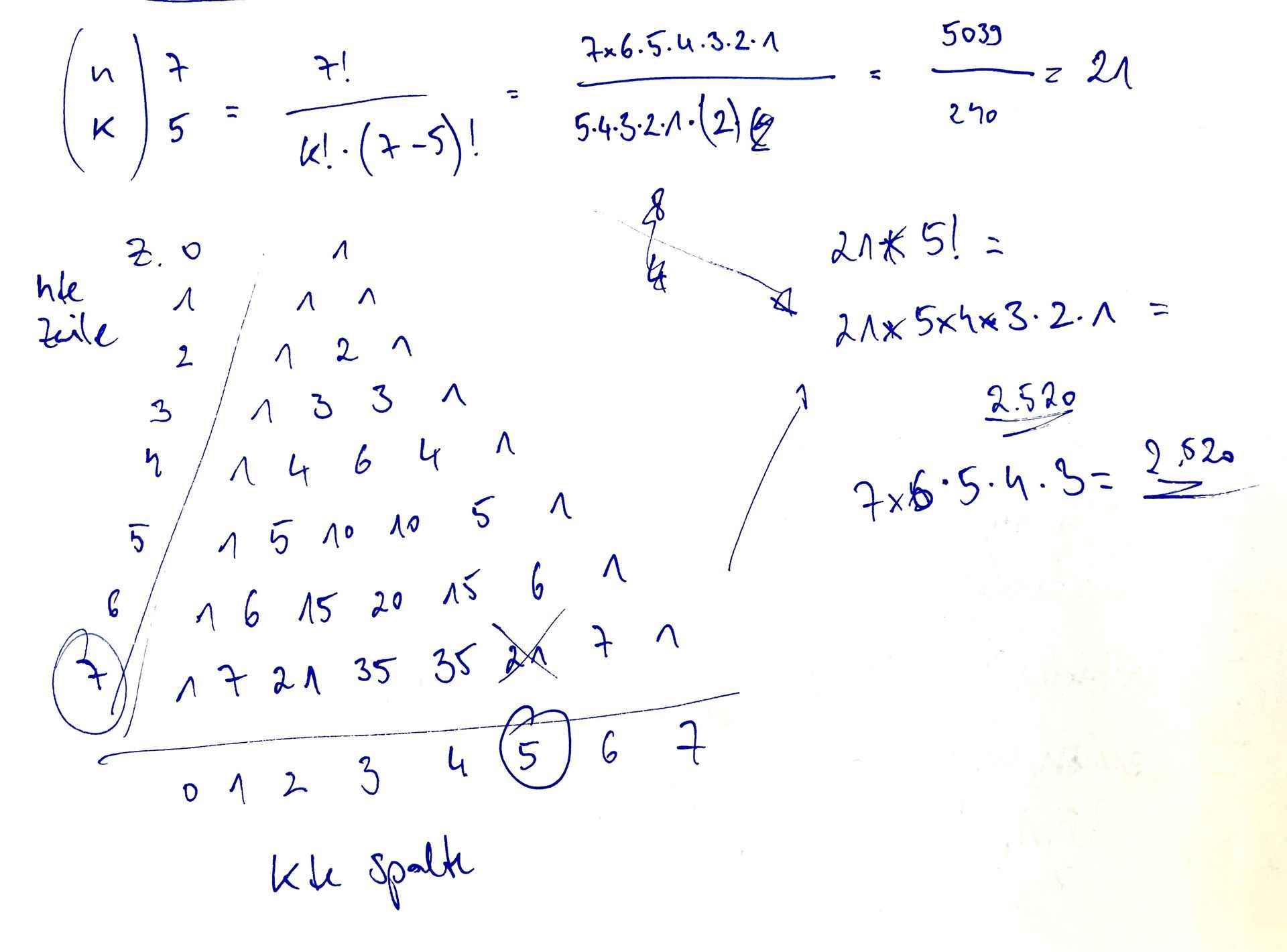
Kombinatorik, Stochastik, da war doch mal was. Genau! Fakultät! Mit Ausrufezeichen! Kennt Ihr noch? Fakultät definiert sich als Produkt aller natürlichen Zahlen (außer Null, weil Null würde ja immer alles kaputt machen), die kleiner sind als die Zahl der Fakultät. 5! ist also 5*4*3*2*1 = 120. Wenn n die Zahl der Ziffern im Pool ist (7) und k die Zahl der vorgegebenen Stellen (5), dann ist das n über k. Ein Binominalkoeffizient. Kennt Ihr noch? Also ich kannte es nicht mehr. Nicht wissen macht nichts - aber einer KI-Suchmaschine die richtigen Fragen stellen musst du können (die bietet dann auch gleich noch Quellen, Übungsaufgaben und Flashkarten mit an) Wikipedia? Wikipedia auf, kurz erschrecken, Wikipedia wieder zu. Wikipedia bleibt unersetzlich als enzyklopädische Sammlung und Wissensbasis, aber da toben sich zu viele Auskenner aus, denen es nicht auf Verständlichkeit und Vermittlung ankommt, sondern auf die Expertentum-Bühne - eine Form von intellektueller Angeberei, die es überall gibt, auch an den Universitäten, wo sie sich (besonders in Deutschland) in einer Kompliziert- und Geschraubtheit von Fachsprache äußert, die eher als Distinktionsmerkmal dient und weniger zur Wissensvermittlung.

Youtube sei Dank! Mathe-Erklärvideos sind Minimum 5-Fakultät leichter zu verstehen (allerdings auch nicht alle) als die entsprechenden Wikipedia-Einträge oder mathematische Lehrbücher. Isso. 7 über 5 ist 21, das lässt sich übrigens nicht nur als Binominalkoeffizient errechnen, sondern alternativ auch mit dem Pascalschen Dreieck. Kennt Ihr noch? Das Problem ist allerdings: Das war's noch nicht. Wer damit begonnen hat, die möglichen Kombinationen systematisch aufzuschreiben, erkennt ziemlich schnell, dass 21 nicht stimmen kann. Der Binominalkoeffizient funktioniert ja auch nur dann, wenn die Reihenfolge egal ist, bei bunten Kugeln zum Beispiel. Bei Zahlen ist die Reihenfolge der Ziffern innerhalb der Zahlen aber ganz und gar nicht egal. Das erhöht die Zahl der möglichen Lösungen ein bisschen: 21*5! = 2.520.

Danach konnte ich mich direkt hinlegen.

Woher ich diese sehr passende Statistik zur Aufgabe habe, habe ich leider vergessen. Sollte die Urheberin sie hier wiedererkennen: gerne melden, dann korrigiere ich die Quellangabe.

👉 kleine Beiträge wie dieser sind Erinnerungen: an reine Freude, die ich empfunden habe - und häufig auch immer wieder, wenn ich sie sehe. Ein ungewöhnlicher Blick, überraschende Sichtweisen und Entdeckungen, inspirierende Kreativität, ein schöner Gedanke, gelungenes Handwerk, schöne Formulierungen, Dinge mit Seele. Sie sind vollkommen zweck- und absichtsfrei - und trotzdem alles andere als sinnlos: Es tut unendlich gut, sich jeden Tag über etwas zu freuen. Und sei es noch so unbedeutend. Enjoy!